Binary Coding
By Sébastien Boisgérault, Mines ParisTech
February 13, 2017
Contents
Binary Data
Digital audio data – stored in a file system, in a compact disc, transmitted over a network, etc. – always end up coded as binary data, that is a sequence of bits.
Bits
Binary Digits and Numbers
The term “bit” was coined in 1948 by the statistician John Tukey as a contraction of binary digit.
It therefore refers to a numeral symbol in base 2: either \(0\) or \(1\). Several binary digits may be used to form binary numbers in order to represent arbitrary integers. In the decimal system (base \(10\)), “\(42\)” denotes \(4 \times 10^1 + 4 \times 10^0\) ; similarly, in base 2, \[b_0 b_1 \cdots b_{n-1} \; \mbox{ where } \; b_i \in \{0,1\}\] represents the integer \[ b_0 \times 2^{n-1} + b_1 \times 2^{n-1} + \cdots + b_{n-1} \times 2^0. \] As an example the number 42 (decimal representation), equal to \(1 \times 2^5 + 0 \times 2^4 + 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 0 \times 2^0,\) has the binary representation \(101010\).

The term “digit” used in the construction of “bit” is somehow self-contradictory as the etymology of “digit” refers to the base ten:
The name “digit” comes from the fact that the 10 digits (ancient Latin digita meaning fingers) of the hands correspond to the 10 symbols of the common base 10 number system, i.e. the decimal (ancient Latin adjective dec. meaning ten) digits.
In Python, the decimal notation is obviously available to define number litterals, but we also may use the prefix 0b to define a number with its binary representation. The built-in function bin returns the binary representation of a number as a string:
>>> 42
42
>>> 0b101010
42
>>> bin(42)
'0b101010'Note that there is not a unique binary representation of an integer: one can add as many leading zeros without changing the value of the integer. The function bin uses a canonical representation of the binary value that uses the minimum number of digits necessary to represent the binary value … except for 0 which is represented as 0b0 and not 0b ! Except for this particular value, the first binary digit (after the prefix 0b) will always be 1. However, sequences of bits beginning with (possibly) multiple \(0\)’s are valid: 0b00101010 is a valid definition of \(42\). Finally, note that negative integers may also be described within this system: \(-42\) is for example denoted as -0b101010.
Several arithmetic operators in Python (operation on numbers), for example <<, >>, |, ^, &, are far simpler to understand when their integer arguments are in binary representation. Consider:
>>> print 42 << 3
336
>>> print 42 >> 2
10
>>> print 42 | 7
47
>>> print 42 ^ 7
45
>>> print 42 & 7
2versus
>>> print bin(0b101010 << 3)
0b101010000
>>> print bin(0b101010 >> 2)
0b1010
>>> print bin(0b101010 | 0b111)
0b101111
>>> print bin(0b101010 ^ 0b111)
0b101101
>>> print bin(0b101010 & 0b111)
0b10To summarize:
<< nis the left shift byn: bits are shifted on the left bynplaces, the holes being filled with zeros,>> nis the right shift byn: bits are shifted on the right bynplaces, bits in excess being dropped,|is the bitwise or: the bits of the two binary numbers are combined place-by-place, the resulting bit being 0 if both bits are 0, and 1 otherwise,^is the bitwise exclusive or (xor):
the bits of the two binary numbers are combined place-by-place, the resulting bit being 1 if exactly one of the bits is 1, and 0 otherwise,&is the bitwise and: the bits of the two binary numbers are combined place-by-place, the resulting bit being 1 if both bits are 1, and 0 otherwise.
Bytes and Words
In many application contexts, we consider binary data as sequences of groups of a fixed number of bits named bytes. Consider for example that every data in computer memory is accessed through pointers and that a pointer gives the location of a byte, not of an individual bit. All the same, filesystems store data into files that contain an entire number of bytes. Despite several historical choices of the size of the byte (due to different hardware architectures), nowadays, the de facto size for the byte is 8 bits, that is the byte is an octet. In the sequel, we will drop the octet term entirely and use byte instead.Bytes are sometimes grouped into even larger structures, called words, that may group 2, 3, 4, etc. bytes. The choice of the size of a word often reflect the design of a specific hardware architecture1.
Alternate Representations - Hexadecimal and ASCII
The hexadecimal representation of an integer uses the base 16. As a consequence, any byte may be represented by an hexadecimal number with two digits. This representation, being more compact than the binary, often makes binary data easier to interpret by human beings. The 10 first hexadecimal digits are represented by the symbols \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\) and the \(5\) following (that correspond to the decimal value \(10\), \(11\), \(12\), \(13\), \(14\), \(15\)) are a, b, c, d, e, f (sometimes capitalized).As an example, here is the representation of a few numbers in decimal, binary and hexadecimal form:
| decimal | binary | hexadecimal |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1100 | B |
| 15 | 11111 | F |
| 16 | 100000 | 10 |
| 42 | 101010 | 2A |
Integer literals in hexadecimal notation are supported in Python with the 0x prefix. For example
>>> 0x10
16
>>> 0xff
255
>>> 0xcaffe
831486In Python 2.x, binary data is also naturally represented as strings, instances of the type str ; reading data from file objects or writing into them is made via a string representation. String are therefore used as the same time to describe text – even if in this case the unicode strings of type unicode are more appropriate – and binary data.
Strings are delimited with quotes. Within the quotes, a byte may be denoted a symbol (letter, digits, punctuation marks, etc.) – in which case the byte value is the ASCII code of the symbol – or by an escape sequence \x?? where ?? is the hexadecimal representation of the byte. The latter case is handy when the symbol that would represent the byte is not printable. For example, "S\xc3\xa9bastien" is the string that represent the text “Sébastien” in the utf-8 text encoding: the e acute does not belong to the set of ASCII printable characters and is represented by the combination of the bytes 0xc3 and 0xa9.
Consider the string made of all characters whose code increases from \(0\) to \(255\). We write it to a file and use the canonical output of the hexdump command to display to file content. The middle columns contain the hexadecimal representation of the data and the right column the character representation. The symbols outside of the printable characters range (hexadecimal 20 to 7F) are replaced with dots.
>>> string = "".join([chr(i) for i in range(256)])
>>> file = open("file.txt", "w")
>>> file.write(string)
>>> file.close()
>>> import os
>>> e = os.system("hexdump -C file.txt")
00000000 00 01 02 03 04 05 06 07 08 09 0a 0b 0c 0d 0e 0f |................|
00000010 10 11 12 13 14 15 16 17 18 19 1a 1b 1c 1d 1e 1f |................|
00000020 20 21 22 23 24 25 26 27 28 29 2a 2b 2c 2d 2e 2f | !"#$%&'()*+,-./|
00000030 30 31 32 33 34 35 36 37 38 39 3a 3b 3c 3d 3e 3f |0123456789:;<=>?|
00000040 40 41 42 43 44 45 46 47 48 49 4a 4b 4c 4d 4e 4f |@ABCDEFGHIJKLMNO|
00000050 50 51 52 53 54 55 56 57 58 59 5a 5b 5c 5d 5e 5f |PQRSTUVWXYZ[\]^_|
00000060 60 61 62 63 64 65 66 67 68 69 6a 6b 6c 6d 6e 6f |`abcdefghijklmno|
00000070 70 71 72 73 74 75 76 77 78 79 7a 7b 7c 7d 7e 7f |pqrstuvwxyz{|}~.|
00000080 80 81 82 83 84 85 86 87 88 89 8a 8b 8c 8d 8e 8f |................|
00000090 90 91 92 93 94 95 96 97 98 99 9a 9b 9c 9d 9e 9f |................|
000000a0 a0 a1 a2 a3 a4 a5 a6 a7 a8 a9 aa ab ac ad ae af |................|
000000b0 b0 b1 b2 b3 b4 b5 b6 b7 b8 b9 ba bb bc bd be bf |................|
000000c0 c0 c1 c2 c3 c4 c5 c6 c7 c8 c9 ca cb cc cd ce cf |................|
000000d0 d0 d1 d2 d3 d4 d5 d6 d7 d8 d9 da db dc dd de df |................|
000000e0 e0 e1 e2 e3 e4 e5 e6 e7 e8 e9 ea eb ec ed ee ef |................|
000000f0 f0 f1 f2 f3 f4 f5 f6 f7 f8 f9 fa fb fc fd fe ff |................|The character representation of most binary data that is not text is going to be meaningless, apart from text tags used to identify the nature of the file, or specific chunks of text data within a heterogeneous data content. For example, the hexdump of the start of a WAVE audio file may look like:
>>> e = os.system(r"hexdump -C -n160 You\ Wanna\ Have\ Babies.wav")
00000000 52 49 46 46 d8 cf 06 00 57 41 56 45 66 6d 74 20 |RIFF....WAVEfmt |
00000010 10 00 00 00 01 00 02 00 44 ac 00 00 10 b1 02 00 |........D.......|
00000020 04 00 10 00 4c 49 53 54 18 00 00 00 49 4e 46 4f |....LIST....INFO|
00000030 49 41 52 54 0c 00 00 00 4a 6f 68 6e 20 43 6c 65 |IART....John Cle|
00000040 65 73 65 00 64 61 74 61 94 cf 06 00 28 ff 2b ff |ese.data....(.+.|
00000050 2b ff 2f ff 34 ff 37 ff 3f ff 3e ff 46 ff 41 ff |+./.4.7.?.>.F.A.|
00000060 48 ff 43 ff 41 ff 3f ff 32 ff 30 ff 15 ff 13 ff |H.C.A.?.2.0.....|
00000070 f1 fe f0 fe cf fe d1 fe bf fe c1 fe c1 fe c1 fe |................|
00000080 cd fe d0 fe de fe e4 fe f5 fe f9 fe 0c ff 0f ff |................|
00000090 24 ff 26 ff 35 ff 35 ff 38 ff 3b ff 2c ff 32 ff |$.&.5.5.8.;.,.2.|
000000a0 1c ff 22 ff 13 ff 16 ff 1b ff 1a ff 36 ff 38 ff |..".........6.8.|
000000b0 5f ff 65 ff 94 ff 96 ff ce ff ca ff ff ff 00 00 |_.e.............|
000000c0 2b 00 2e 00 4b 00 4e 00 59 00 5e 00 57 00 5b 00 |+...K.N.Y.^.W.[.|
000000d0 4a 00 4c 00 43 00 41 00 43 00 42 00 4b 00 4f 00 |J.L.C.A.C.B.K.O.|
000000e0 59 00 5a 00 64 00 62 00 63 00 64 00 5b 00 5d 00 |Y.Z.d.b.c.d.[.].|
000000f0 4f 00 4d 00 3d 00 38 00 1c 00 1b 00 f5 ff fa ff |O.M.=.8.........|
00000100 ce ff d4 ff a8 ff ae ff 7e ff 84 ff 4c ff 52 ff |........~...L.R.|
00000110 18 ff 1b ff ee fe f0 fe d6 fe d8 fe d0 fe d0 fe |................|
00000120 cd fe cf fe c8 fe ca fe c4 fe c0 fe c8 fe c3 fe |................|
00000130 d4 fe d3 fe e8 fe ea fe fd fe ff fe 08 ff 08 ff |................|
00000140Integers
NumPy provide 8 different types to describe integers: uint8, uint16, uint32, uint64, int8, int16, int32 and int64. The digits at the end of the type name denote the size in bits of the representation: all these representations are fixed-size and use an entire number of bytes so that they may be handled efficiently by the hardware. The type whose name start with a “u” are unsigned, they represent only non-negative integers ; the others are signed, they may represent negative integers as well.
We will explain how these types represent integers as binary data. We will use the bitstream library to illustrate this ; more specifically, we will only use its ability to handles bits as sequence of booleans and build on top of that the functions needed to manage the integer types.
Unsigned Integers
The non-negative integers that may be described in one byte are in the range \(0, 1, ..., 255\). Writing them in a binary stream one bit at a time may be done like that:def write_uint8(stream, integers):
integers = array(integers)
for integer in integers:
mask = 0b10000000
while mask != 0:
stream.write((integer & mask) != 0)
mask = mask >> 1The use of the statement integers = array(integers) ensures that single integers, lists of integers and array of integers will all be handled as arrays.
Reading unsigned 8-bit integers from a stream is even simpler:
def read_uint8(stream, n=None):
if n is None:
integer = 0
for _ in range(8):
integer = (integer << 1) + int(stream.read(bool))
return integer
else:
return array([read_uint8(stream) for _ in range(n)], uint8)This code can easily be generalized to handle 16-bits or 32-bits integers.
The audio.bitstream library actually supports these types already, with quite a few extra features – error handling, efficient vectorization, and static typing for extra performance via Cython.
If that was not already done, we could register the above encoder and decoder via
bitstream.register(uint8, reader=read_uint8, writer=write_uint8)The following Python session demonstrates a few ways to write 8-bits unsigned to streams and read them from streams.
>>> stream = BitStream()
>>> stream.write(uint8(0))
>>> stream.write(15, uint8)
>>> write_uint8(stream, 255)
>>> print stream
000000000000111111111111
>>> stream.write([0, 15], uint8)
>>> stream.write([uint8(255), uint8(0)])
>>> stream.write(array([15, 255], uint8))
>>> print stream
000000000000111111111111000000000000111111111111000000000000111111111111
>>> stream.read(uint8)
0
>>> stream.read(uint8, 2)
array([ 15, 255], dtype=uint8)
>>> stream.read(uint8, inf)
array([ 0, 15, 255, 0, 15, 255], dtype=uint8)The first form to write integers – stream.write(uint8(0)) – automatically detects the type of the argument, the second – stream.write(15, uint8) – uses an explicit type argument and is slightly faster. The third one that calls the writer directly and bypasses the call to stream.write – write_uint8(stream, 127) – is again slightly faster. But the real way to make a difference performance-wise is to vectorize these calls and write several integers at once, either lists of integers – as in the calls to stream.write([0, 15], uint8) or stream.write([uint8(255), uint8(0)]) – or better yet write NumPy arrays with data type uint8 as in the call stream.write([15, 255], uint8).
Reading such integers from a stream may be done one integer at at time – as in the call stream.read(uint8) – or many at the same time, the data being packed into NumPy arrays – as in stream.read(uint8, 2), the second argument being the number of integers.
Signed Integers
A first approach to the coding of 8-bit signed integers would be to use the first bit to code the sign and the remaining 7 bits to code the absolute value of the integer.def write_int8(stream, integers):
integers = array(integers)
for integer in integers:
stream.write(integer < 0)
integer = abs(integer)
mask = 0b1000000
while mask != 0:
stream.write((integer & mask) != 0)
mask = mask >> 1
stream.writeIn this scheme, the code 1000000 is never used (it would correspond to \(-0\)), and therefore we could code \(255\) different integers, from \(-127\) to \(127\). By shifting the negative values by \(1\) we could use all 8-bit codes and therefore encode the \(-128\) to \(127\) range. The modification would be:
def write_int8(stream, integers):
integers = array(integers)
for integer in integers:
if integer < 0:
negative = True
integer = - integer - 1
else:
negative = False
stream.write(negative)
mask = 0b1000000
while mask != 0:
stream.write((integer & mask) != 0)
mask = mask >> 1The actual standard coding of 8-bit signed integers uses a slightly different scheme called two’s complement: conceptually, we encode the integer as in the previous scheme but as a last step, the bits other than the sign bits are inverted – 0 for 1, 1, for 0 – for the negative numbers. A careful examination of the code below shows that it implements effectively the desired scheme ; the line 2**8 - integer - 1 actually explains the name of this scheme:
def write_int8(stream, integers):
integers = array(integers)
for integer in integers:
if integer < 0:
integer = 2**8 - integer - 1
mask = 0b10000000
while mask != 0:
stream.write((integer & mask) != 0)
mask = mask >> 1The motivation behind two’s complement schemes is that addition correctly works between signed integers, without any special handling of the bit sign2.
Let’s see the result of this encoding on a few examples:
>>> BitStream(0, int8)
00000000
>>> BitStream(127, int8)
01111111
>>> BitStream(-128, int8)
10000000
>>> BitStream(-127, int8)
10000001
>>> BitStream(-3, int8)
11111101
>>> BitStream(-2, int8)
11111110
>>> BitStream(-1, int8)
11111111Network Order
Consider the integer 3882 ; we need at least two bytes to encode this number in an unsigned fixed multi-byte scheme. Theaudio.bitstream modulde represents this integer as 0000111100101010: the integer 3882 is equal to \(15 \times 2^8 + 42\). We have encoded the 8-bit unsigned integer \(15\) – the most significant bits 00001111 – first and then the least significant bits 00101010. This scheme is called the big endian ordering and this is what the audio.bitstream module support by default. The opposite scheme – the little endian ordering – would encode \(42\) first and then \(15\), and then the bit content would be 0010101000001111.NumPy provides a handy method on its multi-byte integer types: newbyteorder. It allows to switch from a little endian representation to a big endian and reciprocally. See for example:
>>> BitStream(uint16(42))
0000000000101010
>>> BitStream(uint16(42).newbyteorder())
0010101000000000
>>> BitStream(uint32(42))
00000000000000000000000000101010
>>> BitStream(uint32(42).newbyteorder())
00101010000000000000000000000000So reading an integer encoded in little endian representation is done in two steps: read it (as if it was encoded with the big endian representation) and then use the method newbyteorder on the result.
Information Theory and Variable-Length Codes
In this section, we introduce the modelling of sources or channels as random generators of symbols and measure the quantity of information they have. We’ll see later – as anyone can guess – that such a measure directly influences the size of the binary data necessary to encode such sources.
Entropy from first principles
The (Shannon) information content of an event \(E\) is: \[ I(E) = - \log_2 P(E) \]

This expression may actually be derived from a simple set of axioms:
Positivity: the information content has non-negative – finite or infinite – values,
Neutrality: the information content of an event only depends on the probability of the event,
Normalization: the information content of an event with probability \(1/2\) is \(1\),
Additivity: the information content of a pair of independent events is the sum of the information content of the events.
The positivity of the information content is a natural assumption. The value \(+\infty\) has to be allowed for a solution to the set of axioms to exist: it does correspond to events whose probability is \(0\) ; they are so unlikely that their occurence brings an infinite amount of information. More generally, it’s easy to see, given the expression of the informatio content, that the less likely an event is, the bigger its information content is. The additivity axiom is also quite natural but one shall emphasize the necessity of the independence assumption. On the contrary, consider two events \(E_1\) and \(E_2\) that are totally dependent: if the first occurs, we know for sure that the second also will. Then \(P(E_1\wedge E_2) = P(E_1) \times P(E_2 | E_1) = P(E_1)\) and therefore, the information content \(I(E_1)\) is equal to \(I(E_1\wedge E_2)\): the occurence of the second event brings no further information.
The normalization axiom is somehow arbitrary: we could have selected any finite positive value instead of \(1\), but this convention is the most convenient in the context of binary data. This axiom basically says that the probability that a random bit – whose values \(0\) and \(1\) are equally likely – is \(1\) (or \(0\) for that matter) is \(1\). So if we imagine a memory block of \(n\) bits whose values is random and independent, for any sequence of \(n\) values in \(\{0,1\}\), the probability that the memory block has that precise state is \(n\times 1 = n\). With this convention, the information content unit corresponds to the number of bits ! Therefore, it makes sense to use the word “bit” as a basic measure of information content ; Shannon use the word with this meaning as soon as 1948, the year Tukey invented it.
Let’s now prove that the first four fundamental axioms imply that the information content of an event is given by the formula \(I(E) = - \log_2 P(E)\).
Proof.
Let \(f:[0,1] \to [0, +\infty]\) be such that for any event \(E\), we have \(I(E) = f(P(E))\). Let \(E_1\) and \(E_2\) be independent events with \(p_1 = P(E_1)\) and \(p_2 = P(E_2)\). As \(P(E_1 \wedge E_2) = p_1 \times p_2\), we have \[f(p_1 \times p_2) = I(E_1 \wedge E_2) = I(E_1) + I(E_2) = f(p_1) + f(p_2).\] Hence the function \(g = f \circ \exp\) is additive: for any \(x, y \in [-\infty, 0]\), \(g(x + y) = g(x) + g(y)\). As \(g\) takes non-negative values, \(g\) is non-increasing. Moreover, as \(g(- \log 2) = f(1/2) = 1\), it is finite on \((-\infty, 0]\) and satisfies \(g(-\infty) = +\infty\) and \(g(0) = 0\). It is also continous on \((-\infty, 0]\). As \(g(-p/q) = p/q \times g(-1)\) for any \((p,q) \in \mathbb{N} \times \mathbb{N}^{*}\), by continuity, \(g(x) = -x g(-1)\): \(g\) is homogeneous. Precisely, \(g(x) = -({x}/{\log 2}) g(- \log 2) = -{x}/{\log 2}\) and therefore \(f(p) = g \circ \log (p) = - {\log p} / {\log 2} = - \log_2 p\). \(\blacksquare\)Let \(X\) be a discrete random variable. The entropy of \(X\) is the mean information content among all possible outcomes \[ H(X) = \mathbb{E} \left[ x \mapsto I(X=x)\right], \] or explicitly \[ H(X) = - \sum_{x} P (X=x) \log_2 P(X=x) \] If \(X\) takes \(N\) possible different values \(x_1\) to \(x_N\), we can show that the entropy is maximal if \[ P(X=x_1) = \cdots = P(X=x_N) = 1/N \] that is, if the variable \(X\) is “totally random”, all of its values being equally likely. In this case, we have \[ H(X) = \log_2 N \] In particular, if the random variable \(X\) with values in \(\{0, 1, \cdots, 2^n-1\}\) is a model for the state of a memory block of \(n\) bits where all states are equally likely, then \[ H(X) = n \] so once again, it makes sense to attach to the entropy a unit named “bits”.
Password Strength measured by Entropy
Given that entropy measures the quantity of information of a random symbol source, it is an interesting tool to measure the strength of a password. Let’s measure the entropy attached to the first password generation method described in the xkcd strip below; the algorithm generates passwords such as$ ./password.py 5
Ablatival8'
Horseplay>4
greff0tome1*
beelzebub)4
Conta¡nments5.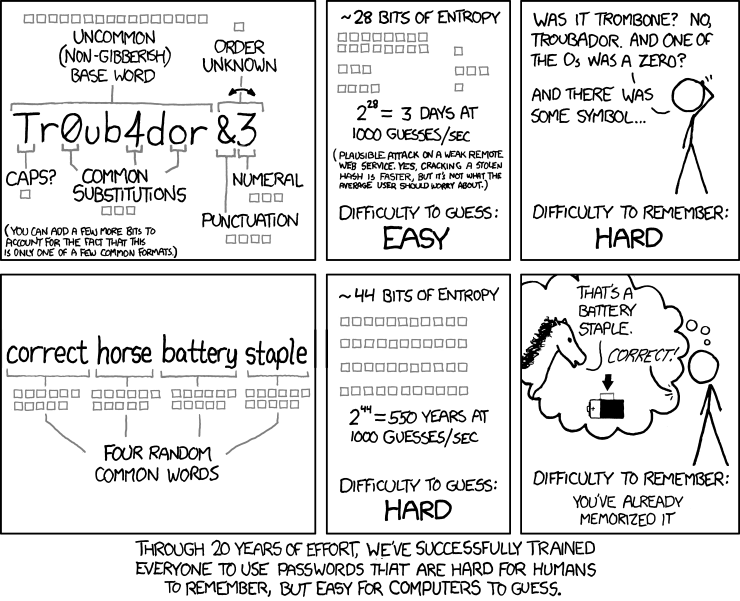
"Tr0ub4dor\&3" or "correct horse battery staple" ? http://xkcd.com/936/Here are the steps that are reproduced:
long and uncommon base word. Pick at random an english word of at least 9 letters. The
words.pyutility gives us the number of such words:$ ./words.py "len(word) >= 9" 67502At this stage, your pick may be:
"troubador"If every word in the dictionary has the same chance to be picked, the entropy of your word generator so far is:
>>> log2(67502) 16.042642627599378So far our estimate closely matches the one from the xkcd comic strip. (16 grey “bit boxes” attached to the base random word).
caps ? Capitalize the word – or don’t – and that randomly (each strategy is equally likely and independent of the previous pick).
You password at this stage may be:
"Troubador"and the corresponding entropy:
>>> log2(67502) + 1 17.042642627599378common substitutions. Let’s pretend that there is a flavor of the “leetspeak” language (see http://en.wikipedia.org/wiki/Leet) where every letter is uniquely represented by an alternate symbol that is unique and not a letter. For example
a\(\rightarrow\)4,b\(\rightarrow\)8,c\(\rightarrow\)(,e\(\rightarrow\)3,l\(\rightarrow\)1,o\(\rightarrow\)0,i\(\rightarrow\)!,t\(\rightarrow\)7,x\(\rightarrow\)\%, etc. so thatleetfor example is represented as1337. Replace letters in position 3, 6 and 8 by their corresponding leetspeak number – or don’t do it – randomly, the two options being equally likely and independent of the previous steps.You password at this stage may be:
"Tr0ub4dor"and the corresponding entropy:
>>> log2(67502) + 1 + 3 20.042642627599378punctuation and numeral. Pick at random a non-letter, non-digit symbol among printable characters in the US-ASCII set. There are \(127\) US-ASCII characters, \(95\) of them are printable (codes
0x20to0x7E(see http://en.wikipedia.org/wiki/ASCII#ASCII_printable_characters), that makes \(95\) minus \(10\) digits minus \(2 \times 26\) letters – lower and upper case – that is \(33\) possible symbols. Add a random digit symbol and optionally swap the punctuation and digit symbols at random.You password at this stage may be:
"Tr0ub4dor&3"and the corresponding entropy:
>>> log2(67502) + 1 + 3 + log2(33) + log2(10) + 1 29.408964841845194
Alphabets, Symbol Codes, Stream Codes
An alphabet is a countable set of distinct symbols, meant to represent information. For example, the letters "a" to "z", all unicode glyphs, the words of the English language, the non-negative integers, the binary values \(0\) and \(1\), etc.
Let \(\mathcal{A}\) be an alphabet and \(n \in \mathbb{N}\). We denote \(\mathcal{A}^n\) the set of all \(n\)-uples with elements in \(\mathcal{A}\), \(\mathcal{A}^+\) the set of all such non-empty \(n\)-uples when \(n\) varies and \(\mathcal{A}^{\ast}\) the set of all such \(n\)-uples, including the (empty) \(0\)-uple denoted \(\epsilon\). \[ \mathcal{A}^n = \; \stackrel{\mbox{$n$ terms}}{\overbrace{\mathcal{A} \times \cdots \times {\mathcal{A}}}}, \; \; \mathcal{A}^+ = \bigcup_{n=1}^{+\infty} \mathcal{A}^n, \; \; \mathcal{A}^{\ast} = \{\epsilon\} \cup \mathcal{A}^+ \] Elements of \(\mathcal{A}^n\) are most of the time denoted without the commas and parentheses, by simple juxtaposition of the symbols of the tuple as in \[ a_0 a_1 \cdots a_{n-1} \in \mathcal{A}^n \] We also talk about sequences and (finite) streams when we refer to such \(n\)-uples. The length of a stream \(a_0 \cdots a_n\) is the number of symbols that it contains: \[ |a_0 \cdots a_{n-1}| = n \] A (variable-length) (binary) symbol code \(c\) is an mapping from an alphabet \(\mathcal{A}\) to the set of non-empty finite binary streams \(\{0,1\}^+\). The code is of fixed length \(n\) if \(c(a)\) has length \(n\) for any \(a \in \mathcal{A}\). We usually require the code to be injective, sometimes using the term non-ambigous code to emphasize this property. The elements of \(\{0,1\}^+\) are named (binary) codes, and valid codes if they belong to the range of \(c\). Such mappings are characterized by: \[ c: \mathcal{A} \to \{0,1\}^+ \; \mbox{ such that } \; c(a) = c(b) \implies a = b \] The non-ambiguity assumption makes the code uniquely decodable: given \(c(a)\), \(a\) is identified uniquely and may be recovered. Symbol codes are usually defined to form stream codes: the mapping \(c\) is extended from \(\mathcal{A}\) to \(\mathcal{A}^+\) by \[ c(a_0a_1 \cdots a_{n-1}) = c(a_0) c(a_1) \cdots c(a_{n-1}) \] The resulting mapping is still a code – with symbols in the alphabet \(\mathcal{A}^+\) instead of \(\mathcal{A}\)) – only if the extended mapping is still non-ambiguous or {bf self-delimiting}, that is, the unique decodability is preserved by the extension to streams. % In order for the stream code is non-ambiguous, the lengths of the valid codes have to satisfy the Kraft inequality: \[ K(c) = \sum_{a \in \mathcal{A}} 2^{-|c(a)|} \leq 1 \] A converse statement also holds, see later.
Proof.
Let \(c\) be a symbol code for \(\mathcal{A}\) whose stream code is non-ambiguous. For any integer \(n\), we have \[ K(c)^n = \sum_{a_0 \in \mathcal{A}} \cdots \sum_{a_{n-1} \in \mathcal{A}} 2^{-(|c(a_0)| + \cdots + |c(a_{n-1})|)} = \sum_{a \in \mathcal{A}^n} 2^{-|c(a)|} \] Assume than \(\mathcal{A}\) is finite and let \(L\) be an upper bound for the code length of symbols in \(\mathcal{A}\). For any integer \(l\), there are at most \(2^l\) distinct binary stream codes whose length is \(l\) and therefore \[ K(c)^n = \sum_{l=n}^{nL} \sum_{{a \in \mathcal{A}^n}{, |c(a)|=l}} 2^{-l} \leq \sum_{l=n}^{n L} 2^l \times 2^{-l} = n (L -1)+ 1 \] Passing to the limit on \(n\) yields \(K(c) \leq 1\). If \(\mathcal{A}\) is countable and \(K(c)>1\), there is a finite subset \(\mathcal{A}'\) of \(\mathcal{A}\) such that \(c' = c|_{\mathcal{A}'}\) satisfies \(K(c') > 1\). Hence, \(c'\) is ambiguous as a stream code and therefore \(c\) also is. \(\blacksquare\)Prefix Codes
Unique decodability is necessary for a code to be useful. Still it does not make the code easy to use. Consider for example the alphabet \(\mathcal{A}= \{0,1,2,3\}\) and the mapping \(\mathcal{A} \to \{0,1\}^+\) \[ 0 \rightarrow 0, \; 1 \rightarrow 01, \; 2 \rightarrow 011, \; 3 \rightarrow 0111 \] It is a code and we can convince ourselves that it is uniquely decodable. However decoding a stream requires lookahead: consider the stream that start by \(010110 \cdots\) and imagine a process that lets you discover the symbols one by one. At the first step, \(0\), you don’t know what the original first symbol is: it could be \(0\), or it could be the partial code for any of the original symbols. So, you have to pick the second symbol, and you can rule out \(0\) but you still can’t decide, the first symbol could be \(1\), or \(2\) or \(3\). Only the third symbol gives you the solution: the stream starts with \(010\) and it can be the case only of the first symbol was \(1\) (with code \(01\)).Given a possible symbol, here, with one step at most we can decide if a code is complete or partial but generally we can build uniquely decodable codes for which this limit is arbitrarily large.
Consider on the contrary the code \[ 0 \rightarrow 0, \; 1 \rightarrow 10, \; 2 \rightarrow 110, \; 3 \rightarrow 1110 \] As soon as you receive a \(0\), the code is complete and you know that you can decode a symbol. Conversely, if you receive a \(1\), you know that you have to keep on reading the bit stream to decode a new symbol. So the decoding process is easy.
Codes that require no look-ahead and are therefore easy to decode are called prefix codes: there is no valid code, that, completed with extra bits, would form another valid code.
So prefix codes make streaming non-ambiguous and easy. However are they general enough ? The answer is yes: if the Kraft inequality is satisfied for a code length function, there is non-ambiguous code that correspond to these lengths, and this code can always be selected to be prefix code. We’ll prove this result later after we have studied the suitable representation of prefix codes.
Example of variable-length code: Unicode and utf-8
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world’s writing systems. The Unicode Consortium, the nonprofit organization that coordinates Unicode’s development, has the ambitious goal of eventually replacing existing character encoding schemes with Unicode and its standard Unicode Transformation Format (UTF) schemes, as many of the existing schemes are limited in size and scope and are incompatible with multilingual environments.
Unicode was developed in conjunction with the Universal Character Set standard and published in book form as The Unicode Standard. As of 2011, the latest version of Unicode is 6.0 and consists of an alphabet of 249,031 characters or graphemes among 1,114,112 possible code points. Code points are designated by the symbol U+X where X is the hexadecimal representation of an integer between 0 to 10ffff. Unicode can be implemented by different character encodings with the most commonly used encoding being UTF-8. UTF-8 uses one byte for any ASCII characters whose code point is between U+00 and U+7f, and up to four bytes for other characters. The coding process is the following: first, if the code point is in the range U+0 – U+7f, the UTF-8 code is \(0\) followed by the code point binary representation. Otherwise, the code point binary representation requires more than \(7\) bits. The UTF-8 code then begins with the unary representation of the number of bytes used to represent the code point given that all bits of the first byte not used by the unary coding may be used and that beyond the first byte, every byte start with 10 which leaves \(6\) usable bits. That is, if the code point binary representation needs \(n\) bits, the number of bytes \(N\) uses by the UTF-8 encoding is \[
N =
1 \, \mbox{ if } \, n \leq 7, \;
\left\lfloor \frac{n-1}{5} \right\rfloor \, \mbox{ if } \, 8 \leq n \leq 31.
\]
The following table summarize the utf-8 code layout.
| Range | Code Format |
|---|---|
U+0 – U+7f |
0xxxxxxx |
U+80 – U+7ff |
110xxxxx 10xxxxxx |
U+800 – U+ffff |
1110xxxx 10xxxxxx 10xxxxxx |
U+100000 – U+1fffff |
11110xxx 10xxxxxx 10xxxxxx 10xxxxxx |
U+200000 – U+3ffffff |
111110xx 10xxxxxx 10xxxxxx 10xxxxxx |
10xxxxxx |
|
U+4000000 – U+7fffffff |
1111110x 10xxxxxx 10xxxxxx 10xxxxxx |
10xxxxxx 10xxxxxx |
As an example, let’s consider the code point U+2203 that represents the character \(\exists\). It is an element of the mathematical operators whose range is U+2200–U+22ff (see http://www.unicode.org/charts/PDF/U2200.pdf). Being in the range U+0800 – U+ffff, it needs 3 bytes to be represented in utf-8. The binary representation of 2203 – as a hexadecimal number – is
00100010 00000011We should fit those \(16\) bits into the \(16\) x slots of the following pattern. No zero padding (adding zeros on the left) is necessary.
1110xxxx 10xxxxxx 10xxxxxxSo, we split the binary representation into
0010 001000 000011and intertwin the result to obtain
11100010 10001000 10000011or in hexadecimal
e2 88 83This is confirmed by the output of the following Python interactive session:
>>> exists = u"\u2203"
>>> print exists
∃
>>> exists.encode("utf-8")
'\xe2\x88\x83'The utf-8 coding may be used in music format to store text information. But given that it really applies to integers, the code point interpretation is sometimes dropped entirely. For example, the FLAC format (http://flac.sourceforge.net/format.html) uses a “utf-8” coding to store sample number and frame number for variable block sizes.
Prefix Codes Representation
Prefix codes may seem to be hard to design. But as a matter of fact suitable representations of such structures make the process quite easy: binary trees and arithmetic representations are here the key structures.Binary Trees
Binary trees are sets of nodes organised in a hierarchical structure where each node has at most two children. Formally, a binary tree is a pair \((\mathfrak{N}, \downarrow)\) where \(\mathfrak{N}\) is a set of elements called nodes and \(\downarrow\) is the children mapping, a partial application \[ \cdot \downarrow \cdot: \mathrm{dom} \, (\downarrow) \subset \mathfrak{N} \times \{0,1\} \to \mathfrak{N} \] such that there exist a unique root node \(r\) \[ \exists \, ! \; r \in \mathfrak{N}, \, \forall \, n \in \mathfrak{N}, \, \forall \, i \in \{0, 1\}, \, r \neq n \downarrow i, \] nodes are not shared \[ n \downarrow i = n' \downarrow i' \; \implies \; i = i' \, \wedge \, b = b' \] and there is no cycle \[ n_0 \downarrow i_0 = n_1, \, \cdots, \, n_{p-1} \downarrow i_{p-1} = n_p \; \implies \; (n_i = n_j \implies i=j). \] A node \(n\) is terminal (or is a leaf node) if it has no children: \[ (n,0) \not \in \mathrm{dom} \,(\downarrow)\; \mbox{ and } \; (n,1) \not \in \mathrm{dom} \,(\downarrow) \] The depth \(|n|\) of a node \(n \in \mathfrak{N}\) is the unique non-negative integer \(d\) defined by \[ \exists \, (b_0, \cdots, b_{|d|-1}) \in \{0,1\}^{|d|}, \; r \downarrow b_0 \downarrow \cdots \downarrow b_{|d|-1} = n. \]Codes are Binary Trees
Let \(\mathcal{A}\) be a finite alphabet and \(c\) a binary code on \(\mathcal{A}\). Let \(\mathfrak{N}\) be the subset of \(\{0,1\}^{\ast}\) of all prefixes of valid codes, that is \[ \mathfrak{N} = \{ b \in \{0,1\}^{\ast}, \; \exists \, b' \in \{0,1\}^{\ast}, \, \exists \, a \in \mathcal{A}, \, c(a) = b b' \} \] We define the children mapping \(\cdot \downarrow \cdot\) by: \[ b_0 \cdots b_{n-1} \downarrow b_n = b_0 \cdots b_{n-1} b_n \] provided that \(b_0 \cdots b_{n-1}\) and \(b_0 \cdots b_{n-1} b_n\) both belong to \(\mathfrak{N}\).With this definition, \((\mathfrak{N}, \downarrow)\) is a binary tree whose root is \(\epsilon\) and the depth of a node is the length of the bit sequence so that the notation used in both contexts \(|b_0\cdots b_{n-1}|\) is not ambiguous. We also define a partial label mapping \(S\) on \(\mathfrak{N}\) with values in \(\mathcal{A}\) by \[ S(b_0\cdots b_{n-1}) = a \; \mbox{ if } \; c(a) = b_0 \cdots b_{n-1} \] \(S\) is a one-to-one mapping from its domain to \(\mathcal{A}\).
Conversely, given a tree \((\mathfrak{N}, \downarrow)\) and a one-to-one partial label mapping \(S\) with values in \(\mathcal{A}\), we may define uniquely a code: let \(r\) be the root node ; for any \(a \in \mathcal{A}\), there is a unique sequence \(b_0 \cdots b_{n-1}\) such that \[ S(r\downarrow b_0 \downarrow b_1 \downarrow \cdots \downarrow b_{n-1}) = a, \] so that we may set \[ c(a) = b_0\cdots b_{n-1} \] In other words, \(c(a)\) is the path from the root node to the node whose label is \(a\).
Binary trees used in this context are usually trimmed down so that all terminal nodes in \(\mathfrak{N}\) are labelled – belong to the domain of \(S\); extra nodes are useless to define the code \(c\). We say that those trees are compact with respect to \(S\) and that \((\mathfrak{N}, \downarrow, S)\) is a (compact, binary, labelled) tree representation of the code \(c\). Among such trees, the ones that correspond to prefix codes are easy to spot: only their terminal nodes are labelled.
Arithmetic representation
Let \(b_0 \cdots b_{n-1} \in \{0,1\}^{n}\). The (binary) fraction representation – denoted \(0.b_0\cdots b_{n-1}\) – of this bit sequence is \[ 0.b_0\cdots b_{n-1} = \sum_{i=0}^{n-1} b_i \times 2^{-i+1}. \] To any such bit sequence \(b\) we may associate an interval in \([0,1)\) by: \[ b = b_0 \cdots b_{n-1} \; \rightarrow \; I(b) = [0.b_0\cdots b_{n-1}, 0.b_0\cdots b_{n-1} + 2^{-n}) \] We may notice that \(I(b)\) is the only interval that contains all binary fractions (whose denominator is a power of two) whose first bits as a binary fraction are \(b_0\), \(\cdots\), \(b_{n-1}\). In other words, it contains the fraction representation of all codes of which \(b_0 \cdots b_{n-1}\) is a prefix. As a consequence, for any prefix code \(c\) on \(\mathcal{A}\) the intervals \(I(c(a))\), \(a\in\mathcal{A}\) are non-overlapping: \[ \forall \, (a, a') \in \mathcal{A}^2, \; a \neq a' \, \implies I(a) \cap I(a') = \varnothing \] This property is actually necessary and sufficient for codes to be prefix codes. We use that crucial property to proof the converse of Kraft’s theorem, namely:Proposition – Kraft Converse Theorem.
Given an alphabet \(\mathcal{A}\) and a list of code lengths \((l_a), \, a \in \mathcal{A}\) such that \[ K = \sum_{a \in \mathcal{A}} 2^{-l_a} \leq 1 \] there is a prefix code \(c\) such that \[ \forall \, a \in \mathcal{A}, \; |c(a)| = l_a \]Proof.
Let’s order all symbols in \(\mathcal{A}\) in a sequence \(a_0\), \(a_1\), \(\cdots\). Given the lengths \(l_a\), \(a \in \mathcal{A}\), we define the sequence of binary fractions and intervals \(x_{a_0}=0\), \(x_{a_n} = x_{a_{n-1}} + 2^{-l_{a_{n-1}}}\) and \(I(a_{n}) = [x_{a_n}, x_{a_{n+1}})\). At any step \(n\) of this process, \(x_{a_n} = \sum_{i=0}^{n-1} 2^{-l_{a_i}} \leq 1\) because Kraft’s inequality holds. We may therefore define the code \(c\) by \[ c(a_n) = b_0\cdots b_{p-1} \; \mbox{ with } \; I(a_n) = [0.b_0\cdots b_{p-1}, 0.b_0\cdots b_{p-1} + 2^{-p}) \] By construction these intervals are non-overlapping and consequently what we have build is a prefix code. \(\blacksquare\)Optimal Length Coding
Given an alphabet and random symbol in it, we explain in this section what bounds exist on codes average bit length and how we can build a code that is optimal for this criteria.
Average Bit Length – Bounds
Let \(\mathcal{A}\) be an alphabet, \(A\) a random symbol in \(\mathcal{A}\) and \(c\) a code on \(\mathcal{A}\). We define the (average) (bit) length of the code as: \[ \mathbb{E} |c(A)| = \sum_{a \in \mathcal{A}} p(a) |c(a)| \] where as usual \(p(a) = P(A=a)\). Let \((\mathfrak{N}, \downarrow, S)\) is a tree representation of \(c\) and define the weight \(w(n) = p(c^{-1}(n))\). The weighted tree \(t=(\mathfrak{N}, \downarrow, S, w)\) has a (weighted) depth \(|t|\) given by \[ |t| = \sum_{n \in \mathrm{dom} \, S} w(n) |n| \] that is equal to \(\mathbb{E} |c(A)|\).We know from the previous section that we can restrict our search to prefix codes. For such codes, the entropy \(H(A)\) provides bounds on the expected length. Specifically, we have:
Proposition.
Every prefix code \(c\) for \(\mathcal{A}\) satisfies \[ H(A) \leq \mathbb{E}sp \, |c(A)|. \] Moreover there exist a prefix code \(c\) for \(\mathcal{A}\) such that \[ \mathbb{E}\, |c(A)| < H(A) + 1. \]Proof.
The mean code length satisfies \[ \mathbb{E} |c(A)| = \sum_{a \in \mathcal{A}} p(a) |c(a)| = - \sum_{a \in \mathcal{A}} p(a) \log_2 2^{-|c(a)|} \] Given the definition of the implicit probability \[ q(a) = \frac{2^{-|c(a)|}}{\sum_{a\in\mathcal{A}} 2^{-|c(a)|}} = \frac{2^{-|c(a)|}}{K(c)}, \] we end up with \[\begin{eqnarray*} \mathbb{E} |c(A)| &=& - \sum_{a \in \mathcal{A}} p(a) \log_2 q(a) - \log_2 K(c) \\ &=& - \sum_{a \in \mathcal{A}} p(a) \log_2 p(a) - \sum_{a \in \mathcal{A}} p(a) \log_2 \frac{q(a)}{p(a)} - \log_2 K(c) \\ &=& H(A) + D(p || q) - \log_2 K(c) \\ &\geq& H(A) \\ \end{eqnarray*}\]For any \(a\in \mathcal{A}\), we define \(l(a) = \lceil - \log_2 p(a) \rceil\). As we have \[ \sum_{a \in \mathcal{A}} 2^{-l(a)} \leq \sum_{a \in \mathcal{A}} 2^{\log_2 p(a)} = \sum_{a \in \mathcal{A}} p(a) = 1 \] there is a prefix code \(c\) that satisfies \(|c(a)| = l(a)\) for any \(a \in \mathcal{A}\). Moreover \[ \mathbb{E} |c(A)| = \sum_{a \in \mathcal{A}} p(a) l(a) < \sum_{a \in \mathcal{A}} p(a) (- \log_2 p(a) + 1) = H(A) + 1. \] \(\blacksquare\)
Algorithm and Implementation of Huffman Coding
We represent (finite) alphabets and the probability distribution of a random symbol as a single Python dictionary, for example \[ \mathcal{A} = \{\mbox{`$a$'}, \mbox{`$b$'}, \mbox{`$c$'}\} \; \mbox{ and } \; p(\mbox{`$a$'}) = 0.5, \; p(\mbox{`$b$'}) = 0.3, \; p(\mbox{`$c$'}) = 0.2 \] as {‘a’: 0.5, ‘b’: 0.3, ‘c’: 0.2}Probabilities will be used as relative weights: instead we could define the dictionary as
{'a': 5, 'b': 3, 'c': 2}and the code resulting from the Huffman algorithm would be the same.
The algorithm we implement uses weighted binary trees where:
terminal nodes are symbol/weight pairs such as
('a', 1.0)non-terminal nodes are children/weight pairs where children is a list of (terminal or non-terminal) nodes, such as
([('c': 0.2), ('a': 0.5)], 0.7)
Handling of these structures is made through a small set of helper functions:
class Node(object):
"Function helpers to manage nodes as (symbol, weight) pairs"
@staticmethod
def symbol(node):
return node[0]
@staticmethod
def weight(node):
return node[1]
@staticmethod
def is_terminal(node):
return not isinstance(Node.symbol(node), list)The Huffman algorithm is the following: we create a list of symbol/weight nodes from the initial dictionary and repeat the following steps:
pick up two nodes with the least weights, remove them from the list,
insert into the list a non-terminal nodes with those two nodes as children and a weight that is the sum of their weights,,
stop when there is a single node in the list: this is the root of the binary tree
Note that this algorithm is not entirely deterministic if at any step, the lowest weight correspond to three nodes or more.
Here is the corresponding implementation in make_binary_tree; note that in the other methods of the huffman class, we also create a symbol to code dictionary (self.table) from the binary tree to simplify the coding and decoding of symbols – not all functions are given in this chunk of code ; the symbol_encoder and symbol_decoder create (symbol) coders and decoders from the symbol to code tables and stream_encoder and stream_decoder create stream coder and encoder from those.
class huffman(object):
def __init__(self, weighted_alphabet):
self.weighted_alphabet = weighted_alphabet
self.tree = huffman.make_binary_tree(weighted_alphabet)
self.table = huffman.make_table(self.tree)
self.encoder = stream_encoder(symbol_encoder(self.table))
self.decoder = stream_decoder(symbol_decoder(self.table))
@staticmethod
def make_binary_tree(weighted_alphabet):
nodes = weighted_alphabet.items()
while len(nodes) > 1:
nodes.sort(key=Node.weight)
node1, node2 = nodes.pop(0), nodes.pop(0)
node = ([node1, node2], Node.weight(node1) + Node.weight(node2))
nodes.insert(0, node)
return nodes[0]
@staticmethod
def make_table(root, table=None, prefix=None):
if prefix is None:
prefix = BitStream()
if table is None:
table = {}
if not Node.is_terminal(root):
for index in (0, 1):
new_prefix = prefix.copy()
new_prefix.write(bool(index))
new_root = Node.symbol(root)[index]
huffman.make_table(new_root, table, new_prefix)
else:
table[Node.symbol(root)] = prefix
return tableAs usual, the coder and decoder are registered for use with the BitStream instances.
bitstream.register(huffman, reader=lambda h: h.decoder, writer=lambda h: h.encoder)Optimality of the Huffman algorithm
We prove in this section that the Huffman algorithm creates a code whose average bit length is minimal among all prefix codes (and therefore all non-ambiguous stream codes).Switching nodes.
Consider a weighted tree \(t=(\mathfrak{N}, \downarrow, S, w)\) and two of its terminal nodes \(n_1\) and \(n_2\). Switch the position of these nodes and call the resulting tree \(t'\). A simple computation shows that the weighted bit length of \(t'\) is given by \[ |t'| = |t| + (|n_1|_t - |n_2|_{t})(w(n_2) - w(n_1)) \] Consequently, a tree that has a terminal node with a high probability at a depth larger than another node with low probability higher in the tree can’t be optimal, because switching the two nodes would decrease the code average bit length. The same formula also shows that given two terminal nodes \(n_1\) and \(n_2\) among the ones with the lowest probability, we can always find an optimal tree with them as siblings at the greatest depth: at least one optimal tree exist for combinatorial reasons ; for such a tree, either a node is a leaf, or it has two children nodes; now get at the bottom of the tree: there are two terminal nodes. If they are not the desired nodes, switches that are neutral to the average bit length will create a new optimal tree with the desired property.Length optimality.
The proof that the Huffman coding algorithm is optimal is made by induction on the number of symbols. The check for the basis assumption is straightforward. Now assume that the result holds for \(N\) symbols and pick an alphabet with \(N+1\) symbols. Let \(t\) be the tree that results from the application of the Huffman algorithm. Now consider the initial set of symbols and replace the two with the lowest weight (nodes \(n_1\) and \(n_2\)) with a single one with a weight equal to the sum of the original symbol weights. Let \(t'\) be the result of the Huffman algorithm on these \(N\) symbols. The average bit length of both trees are related by \(|t'| = |t| + (w(n_1) + w(n_2)) (|n_1|_t - 1) - w(n_1) |n_1|_t - w(n_2) |n_2|_t = |t| - w(n_1) - w(n_2)\). Now consider an optimal rearrangement of \(t_{\star}\) of \(t\) that would have \(n_1\) and \(n_2\) as siblings at the lowest level (possible by the previous section). Grouping \(n_1\) and \(n_2\) leads to a \(t'_{\star}\) whose length is \(|t'_{\star}| = |t_{\star}| - w(n_1) - w(n_2)\) and such \(t'_{\star}\) is a rearrangement of \(t'\). Hence, as \(|t| = |t_{\star}| - (|t'_{\star}| - |t'|)\) and because by the induction hypothesis \(t'\) is optimal, \(|t'_{\star}| - |t'| \geq 0\), we have \(|t| \leq |t^{\star}|\) and \(t\) is optimal.Example: Brainfuck, Spoon and Fork
Brainfuck is an eight-instruction Turing-complete programming language. The eight instructions are represented by the characters:> \;\; < \;\; + \;\; - \;\; . \;\; , \;\; [ \;\; ]The language is organised around a single byte pointer p. As an exemple, the instruction “+' corresponds to the C code fragment "(*p)++;" and ".’ to “putchar(*p);”. The classic “Hello World!” program in Brainfuck is the sequence:
++++++++++[>+++++++>++++++++++>+++>+<<<<-]
>++.>+.+++++++..+++.>++.<<+++++++++++++++.
>.+++.------.--------.>+.>.Spoon is a variant of Brainfuck created in 1998 by Steven Goodwin. It uses binary encoding of the eight original symbols according to the mapping
> \(\rightarrow\) 010 |
< \(\rightarrow\) 011 |
+ \(\rightarrow\) 1 |
- \(\rightarrow\) 000 |
. \(\rightarrow\) 001010 |
, \(\rightarrow\) 0010110 |
[ \(\rightarrow\) 00100 |
] \(\rightarrow\) 0011 |
The code is a prefix code that was actually designed using Huffman encoding, with probabilities of each command computed from a set of example programs. You may notice that the code appears NOT to be optimal as , has the longest code and has no sibling: it could be shortened to \(001011\). But that’s only because the actual Spoon variant of Brainfuck introduces two extra reserved codes, \(00101110\) to dump the memory (for debug purposes) and \(00101111\) to stop execution. The full binary tree of the code – where the corresponding symbols are * and ! – and the arithmetic representation are displayed in figure .
The Spoon encoding of the “Hello World!” program is a sequence of 245 bits:
11111111110010001011111110101111111111010111010101
10110110110000011010110010100101001010111111100101
00010101110010100101100101001101111111111111111100
10100100010101110010100000000000000000000010100000
000000000000000000000010100101001010010001010As the commands are exactly \(8\), it is also tempting to define a 3-bit fixed-length encoding of the original symbols and let’s call it Fork ! We adopt the mapping:
> \(\rightarrow\) 000 |
< \(\rightarrow\) 001 |
+ \(\rightarrow\) 010 |
- \(\rightarrow\) 011 |
. \(\rightarrow\) 100 |
, \(\rightarrow\) 101 |
[ \(\rightarrow\) 110 |
] \(\rightarrow\) 111 |
The encoding with Fork of the “Hello World!” program is
01001001001001001001001001001011000001001001001001
00100100000100100100100100100100100100100000100100
10000010001001001001011111000010010100000010100010
01001001001001001010010001001001010000001001010000
10010100100100100100100100100100100100100100100101
00000100010010010100011011011011011011100011011011
011011011011011100000010100000100a stream of 333 binary digits, about 36 % less space-efficient than spoon.
Golomb-Rice Coding
Optimality of Unary Coding – Reduced Sources
Consider the alphabet \(\mathbb{N}\) of the non-negative integers and a random symbol \(n\) in \(\mathbb{N}\) such that for any integer \(i\) \[ P(n=i) = P(n>i) \] Normalization of this probability distribution \(p(i) = P(n=i)\) yields \[ \forall \, i \in \mathbb{N}, \, p(i) = 2^{-i-1} \] What is the optimal coding of such a random symbol ? An infinite number of symbols have a non-zero probability, therefore we can’t apply directly Huffman coding. However, we can get a flavor of what the optimal coding can be by reducing the random symbol to a finite alphabet. To do so, we select a threshold \(m\) and group together all the outcomes of \(n\) greater or equal to \(m\); the new random symbol based on \(n\) has values in the finite alphabet whose symbols are \(0\), \(1\), \(2\), \(\cdots\), \(m-1\) and the set \(\{m,m+1,\cdots\}\) of values above \(m\). The probability of the \(m\) first \(m\) symbols \(i\) is \(p_m(i) = P(n=i) = 2^{-i-1}\) and the probability of the last one is \[ p_m(i) = P(n \geq m) = \sum_{i=m}^{+\infty} P(n=i) = \sum_{i=m}^{+\infty} 2^{-i-1} = 2^{-m} \] Let’s apply the Huffman algorithm to the resulting symbol, say for \(m=2\). Here are the steps that build the Huffman binary tree: the initial list of symbols, sorted by increasing probability is:The nodes \(\{3,4,\cdots\}\) and \(2\) have the lowest probability of occurence and therefore shall be grouped. But their probability is the same – \(0.125\) – and we need to make the a decision about which one will be taken as the first node of the group. We decide to go for the infinite set of symbols \(\{3,4,\cdots\}\) first. Somehow it feels the right thing to do, to have the only compound symbol on the left and all the others on the right …
This group has a cumulative probability of \(0.25\), the same as the symbol \(1\). There is only one extra symbol, \(0\) and its probability is higher, therefore no reordering is necessary. We therefore group \(\{2,3,\cdots\}\) (first) and \(1\).
There are only two symbols left, so the algorithm has completed. Let’s look at the results in terms of coding: we ended up with the code \[ 0 \rightarrow 1, \; 1 \rightarrow 01, \; 2 \rightarrow 001, \{3,4,\cdots\} \rightarrow 000 \] From this we can guess what the optimal coding is for the original source, without the reduction attached to the threshold : it is the unary coding of the integer, or more precisely here, the variant that uses \(0\) for the length and \(1\) as an end symbol. \[ 0 \rightarrow 1, \; 1 \rightarrow 01, \; 2 \rightarrow 001, \; 3 \rightarrow 0001, \; 4 \rightarrow 00001, \; 5 \rightarrow 000001, \; \cdots \]
The choice of the variant has no impact on the optimality of the code: unary coding is the optimal solution for the coding of non-negative integers that occur with a probability \(p(i) = 2^{-i-1}\). Here is an implementation of unary coding of integer symbols that uses \(0\) as an end delimiter instead:
def unary_symbol_encoder(stream, symbol):
return stream.write(symbol * [True] + [False], bool)
def unary_symbol_decoder(stream):
count = 0
while stream.read(bool) is True:
count += 1
return countGiven those symbol encoder and decoder function, the higher-order function stream_encoder and stream_decoder from the coding module generate a stream encoder and decoder respectively.
unary_encoder = stream_encoder(unary_symbol_encoder)
unary_decoder = stream_decoder(unary_symbol_decoder)Finally, we define an empty class unary as a type used to register the encoder and decoder in the bitstream module.
class unary(object):
pass
bitstream.register(unary, reader=unary_decoder, writer=unary_encoder)After that last step, using unary coding and decoding is as simple as:
>>> stream = BitStream()
>>> stream.write([0,1,2,3], unary)
>>> print stream
0101101110
>>> stream.read(unary, 4)
[0, 1, 2, 3]Optimal Coding of Geometric Distribution - Rice Coding
The same method of source reduction may be applied to analyze optimal code for more complex distribution, for example the (one-sided) geometric distribution. Such a distribution is defined by \(p(i) \propto \theta^{i}\) for a \(\theta \in (0,1)\); note that the distribution of the previous section was the special case of \(\theta=0.5\). The normalization of this distribution leads to \[ p(i) = (1-\theta) \theta^i \] The method of reduced source illustrated in the previous section may be used to derive an optimal coding in the general case. Let’s summarize the findings of ; first, let \(l\) be the unique integer such that \[ \theta^l + \theta^{l+1} \leq 1 < \theta^{l-1} + \theta^l. \] The optimal coding of the non-negative integer \(i\) is made of two codes:- the unary coding of \(\lfloor i/l \rfloor\), -the Huffman coding of \(i \mbox{ mod } l\).
The probability distribution needed to perform the second part of the encoding is: \[ P(i \mbox{ mod } l) = \frac{(1-\theta)\theta^i}{1-\theta^l}. \] Note that this distribution is quite flat with respect to the original one. For that reason, the length of the optimal coding are almost constant for the Huffman part. Precisely, the length of the coding of \(0 \leq i < l\) is \(\lfloor \log_2 l \rfloor\) (if \(i< 2^{\lfloor \log_2 l + 1\rfloor} - l\)) or \(\lfloor \log_2 l \rfloor +1\) (otherwise). In particular, if \(l\) is a power of two, we have \(2^{\lfloor \log_2 l + 1\rfloor} - l = l\) is therefore every \(0 \leq i < l\) is coded with the same length of \(\log_2 l\).
Rice Coding
Rice coding (or **Golomb-Power-Of-Two (GPO2) coding)
It uses the remark above to simplify the coding at the price of a usually negligible suboptimality: instead of the “true” integer \(l\), solution of (), we select an approximation of it \(l'=2^n\) that is a power of two, then perform the coding using this value instead of \(l\). As a consequence, the Huffman coding of the second part is replaced by a fixed-length encoding of an integer on \(n\) bits.The remaining issue is to determine a good selection of the Golomb parameter \(n\) ; this issue is described in details in . Initially, we need an estimate of \(\theta\) – that is a priori unknown – from experimental data; we can usually derive it from the mean \(m\) f the available values : as the expectation of a one-sided geometric random variable with parameter \(\theta\) has an expectation of \(\theta/(1-\theta)\), it makes sense to select \[ \theta = \frac{m}{1+m} \] Given the golden ratio \[ \phi = \frac{1 +\sqrt{5}}{2}, \] we select as the number of bits dedicated to the fixed-length coding the value: \[ n = \max \left[0, 1 + \left\lfloor \log_2 \left( \frac{\log (\phi -1)}{\log \theta} \right) \right\rfloor \right]. \]
Implementation
We begin with the definition of arice class that holds the parameters of a given Rice encoding and also provide a method for the selection of the optimal parameter. The use of this method is optional: given that Rice coding is very often applied to distributions of integers that are not geometric, there is no guarantee in general that the Golomb parameter of this method will be the most efficient selection.The parameter n in the rice constructor is the Golomb parameter. The optional signed option may be used to enable the coding of negative integers.
class rice(object):
def __init__(self, n, signed=False):
self.n = n
self.signed = signed
@staticmethod
def select_parameter(mean):
golden_ratio = 0.5 * (1.0 + numpy.sqrt(5))
theta = mean / (mean + 1.0)
log_ratio = log(golden_ratio - 1.0) / log(theta))
return int(maximum(0, 1 + floor(log2(log_ratio))))The following encoder and decoder implementations demonstrate how we deal with signed values: by prefixing the code stream with a bit sign (0 for \(+\), 1 for \(-\)) before we encode the absolute value of the integer. More complex schemes – that intertwin negative and positive values – are possible and may be useful to deal with two-sided geometric distribution that are not centered around \(0\) (see for example ). We then encode the fixed-length part of the code and follow with the unary code.
In the following code, options is meant to be an instance of the rice class, stream is an instance of BitStream and symbol an integer.
def rice_symbol_encoder(options):
def encoder(stream, symbol):
if options.signed:
stream.write(symbol < 0)
symbol = abs(symbol)
remain, fixed = divmod(symbol, 2 ** options.n)
fixed_bits = []
for _ in range(options.n):
fixed_bits.insert(0, bool(fixed % 2))
fixed = fixed >> 1
stream.write(fixed_bits)
stream.write(remain, unary)
return encoder
def rice_symbol_decoder(options):
def decoder(stream):
if options.signed and stream.read(bool):
sign = -1
else:
sign = 1
fixed_number = 0
for _ in range(options.n):
fixed_number = (fixed_number << 1) + int(stream.read(bool))
remain_number = 2 ** options.n * stream.read(unary)
return sign * (fixed_number + remain_number)
return decoderFinally, the rice class, its encoder and decoder are registered for integration with the BitStream instances.
rice_encoder = lambda r: stream_encoder(rice_symbol_encoder(r))
rice_decoder = lambda r: stream_decoder(rice_symbol_decoder(r))
bitstream.register(rice, reader=rice_decoder, writer=rice_encoder)The following Python session demonstrates the basic usage:
>>> data = [0, 8, 0, 8, 16, 0, 32, 0, 16, 8, 0, 8]
>>> rice.select_parameter(mean(data))
3
>>> stream = BitStream()
>>> stream.write(data, rice(3))
>>> stream
000000010000000010000110000000011110000000011000010000000010
>>> stream.read(rice(3), 12)
[0, 8, 0, 8, 16, 0, 32, 0, 16, 8, 0, 8]On this particular data, the selection of the Golomb parameter was effective if we consider the following test of possible parameter values between \(0\) (unary coding) and \(6\).
>>> for i in range(7):
... stream = BitStream(data, rice(i))
... print "rice n={0}: {1} bits".format(i, len(stream))
...
rice n=0: 108 bits
rice n=1: 72 bits
rice n=2: 60 bits
rice n=3: 60 bits
rice n=4: 64 bits
rice n=5: 73 bits
rice n=6: 84 bits